
오늘날 대부분의 렌더러에서 사용되는 Monte Carlo 근사식이다.
한 점 x에서 방향 ωo로 나가는 출사복사도 Lo는,
여러 방향 ωi에서 들어오는 빛 Li와 BRDF fr 및 입사각의 코사인 cos(θi)를 곱해 평균내어 구한다.
이 식은 바로 렌더링 이퀘이션을 샘플 기반으로 근사한 형태이며,
하나의 경로(샘플)당 기여도를 구하는 기본적인 path tracing 수식이다.
렌더링 방정식에서 fr은 BRDF로, 표면에서 빛이 어떻게 반사되는지를 수학적으로 표현하는 항이다.

입사 복사도 대비 출사 복사도의 비율
쉽게 말해, 얼마나 입사된 빛을 반사시키는지를 방향별로 표현한 확률 밀도 함수
하지만 그 전에, 빛의 반사란 무엇인지 먼저 정리해보자.
반사의 네 가지 기본 타입
빛이 표면에서 반사되는 방식은 결국 시각적으로 어떤 느낌을 주느냐로도 구분할 수 있다.
PBRT 책에서는 반사를 크게 네 가지로 분류한다:
- Diffuse (난반사)
→ 모든 방향으로 골고루 퍼지는 반사.
→ 예: 분필판, 무광 페인트 - Glossy Specular (글로시 반사)
→ 특정 방향으로 뿌옇게 반사되는 형태.
→ 예: 유광 플라스틱, 자동차 도장 - Perfect Specular (완전한 정반사)
→ 하나의 방향으로만 정확하게 반사.
→ 예: 유리, 거울 - Retroreflective (역반사)
→ 들어온 방향 그대로 거의 반사되는 형태.
→ 예: 벨벳, 달 표면, 도로 반사 테이프
Lambertian BRDF - Diffuse
모든 방향으로 균일하게 빛을 반사하는 이상적인 확산 모델
현실에서도 무광 페인트, 종이, 분필판 같은 표면에서 꽤 잘 작동함
BRDF는 단순히 상수값:

- : 알베도 (0~1 사이 값, 얼마나 반사되는가)
- π: 단위 반구 전체에 고르게 분포시키기 위한 정규화 상수
이 상수를 곱해줘야 총 반사량이 R이 되도록 맞춰짐

- H2: 노멀 방향 위의 반구 영역 (입사 방향 전부)
- f: BRDF 값. 여기선 Lambertian BRDF, 즉 상수 R/
- cosθ′: 입사각 조명에서 항상 들어감
- dω: 입사 방향 위에서 적분
- 결과적으로 → 총 반사되는 빛의 양이 R (albedo)
-> 반구에서의 적분결과가 R이 되어야만 하므로 항상 π가 나눠짐
렌더링 방정식을 Monte Carlo로 근사할 때, 샘플 방향을 어떻게 고르느냐가
노이즈, 수렴 속도, 퀄리티에 직접적인 영향을 준다.
BRDF 자체는 일정값 R/
하지만 렌더링 방정식에서는 항상 cosθ 항과 곱해져서 사용됨
즉, 실제로 중요한 건 cosθ가 클수록 기여가 크다는 점.
그래서 Cosine-weighted Hemisphere Sampling을 사용한다.
- 가 큰 방향일수록 더 자주 샘플됨
- 샘플을 효율적으로 뽑아 노이즈를 줄일 수 있음
Cosine-weighted Hemisphere Sampling
렌더링 적분에서는 cosine-weighted 방향을 샘플링해야 하지만
반구 표면 위에서 직접 코싸인 분포를 따르는 방향을 샘플링하는 것은 복잡하므로
Malley’s Method를 사용한다.
Malley’s Method
1. x-y평면상의 단위 디스크에서 균일하게 (x, y)를 샘플링한다.
2. 반구로 올린다.
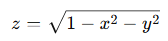
3. 결과적으로 벡터 (x, y, z)가 노멀기준 hemisphere 위에 있고, 그 분포는 정확히 cosθ 비례 분포를 따른다.
vec3 sampleCosineHemisphere(float u1, float u2) {
float r = sqrt(u1);
float theta = 2.0 * 3.14159265 * u2;
float x = r * cos(theta);
float y = r * sin(theta);
float z = sqrt(max(0.0, 1.0 - x * x - y * y));
return vec3(x, y, z);
}
float CosineHemispherePDF(float cosTheta) {
return cosTheta * InvPi;
}
Specular Reflection
Lambertian처럼 모든 방향으로 퍼지지 않고, 오직 한 방향으로만 빛을 반사하는 이상적인 재질이 있다.
바로 거울과 유리 같은 완전한 정반사(perfect specular) 재질이다.
이 경우 BRDF는 델타 함수 형태를 띄며,
빛은 정확히 반사되는 방향으로만 이동하므로 샘플링이 아니라 계산으로 방향을 구한다.
Perfect Specular BRDF
- 입사 방향이 wi, 표면 법선이 n이라면
- 출사 방향 wo = reflect(wi, n) 으로 딱 정해짐.
- 따라서 확률 분포를 기반으로 하는 일반적인 샘플링은 필요 없다.
반사 함수는 다음처럼 표현된다:
이때 중요한건
델타 함수 특성상 BRDF * cosθ / pdf 항이 직접 계산되는 게 아니라,
렌더러 내부에서 델타 적분을 생략하고 그 방향만 따르는 방식으로 처리한다는 점이다.
현실의 대부분의 표면은 완전한 정반사보단 거칠고 퍼진 반사를 가진다.
따라서 이후에는 이 개념을 러프니스 기반의 microfacet 모델로 일반화한다.
Fresnel 반사
빛은 표면에 닿을 때, 일부는 반사되고 일부는 굴절된다.
얼마나 반사되고, 얼마나 투과되는지는 입사각과 재질의 굴절률(IOR) 에 따라 결정된다.
이 비율을 계산하는 것이 바로 Fresnel 방정식이다.
완전 반사면이 아니어도, 입사각이 커지면 반사가 강해지는 현상(Glancing Angle)이 발생한다.
유리, 물 같은 재질을 더 현실감 있게 표현하려면 Fresnel 반사는 필수.
특히 Microfacet BRDF에서는 항상 Fresnel 항이 들어간다.
실용적인 계산 방법: Schlick 근사식
렌더링에서는 복잡한 물리식을 쓰기보단, 간단한 근사식을 사용한다.
그 중 가장 많이 쓰이는 것이 바로 Schlick's Approximation이다:
vec3 fresnelSchlick(float cosTheta, vec3 F0) {
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
F0 = mix(vec3(0.04), albedo, metallic);- cosTheta: 시야 방향과 노멀의 내적값
- F0: 입사각 0도(정면)일 때의 반사율
Microfacet 기반 BRDF로의 확장
실제 세계의 대부분의 재질은 현미경적으로 보면 거칠다.
Microfacet 이론이란?
Microfacet 이론은 이러한 거친 표면을 무수히 많은 미세한 거울 조각(microfacet) 으로 모델링한다.
- 각 microfacet마다 독립적인 노멀 방향을 가진다.
- 카메라에서 보면 이 모든 조각이 하나의 표면처럼 보이지만,
- 빛의 반사 방향은 microfacet의 노멀들에 의해 산란되며 다양한 방향으로 분포하게 된다.
이를 통해 우리는 다음과 같은 두 가지 요소를 구분하게 된다:
- Macro-surface (대표면): 실제 geometry가 가진 전체적인 법선 방향
- Micro-surface (소표면): 그 위에 있는 통계적 분포로 정의된 microfacet 법선들
왜 Microfacet 모델이 필요한가?
PBRT 같은 렌더러도 사실 '거친 표면'을 그냥 초고해상도 메시로 정밀하게 모델링해서,
정반사 BxDF만으로도 결과를 낼 수는 있다.
하지만 이 방식에는 치명적인 문제가 있다:
1. 저장 공간 & 레이 트레이싱 비용 폭증
- 미세한 표면 거칠음을 삼각형 메시로 표현하려면 어마어마한 버텍스 수가 필요하다.
- 이는 저장 용량뿐만 아니라 레이 교차 테스트 비용도 크게 늘어난다.
2. Monte Carlo 효율성 저하
- 완벽한 정반사 모델은 Dirac delta를 포함하므로,
일반적인 BSDF 평가 (즉, f() 함수로 값을 직접 구하는 것)가 불가능하다. - 따라서 샘플링만 가능하고, light sampling (빛이 오는 방향 기반 샘플링) 같은 고급 기법을 못 쓴다.
Microfacet 이론의 통계적 접근
Microfacet 모델은 표면의 미세한 거칠음을 통계적 분포로 모델링한다.
즉, 수많은 미세 거울 조각들이 어떤 방향을 향하고 있는지를
확률 분포로 대체하여 모델링한다는 개념이다.
이 방식은 다음의 두 문제를 모두 해결한다:
- 디테일한 지오메트리를 저장할 필요가 없다.
- Dirac delta 대신 연속적인 분포를 사용하므로 Monte Carlo 샘플링이 훨씬 쉬워진다
Microfacet 모델이 고려해야 할 세 가지 효과
- Masking
→ 어떤 microfacet이 카메라 시점에서 다른 조각에 가려질 수 있음 - Shadowing
→ 어떤 microfacet에 빛이 닿기 전에 다른 조각에 가려짐 - Interreflection
→ 빛이 microfacet 사이에서 반사 반사를 반복한 후 관측점에 도달
Microfacet Distribution Function (NDF)
표면 거칠기(roughness)를 통계적으로 모델링하는 핵심 함수
실제 거친 표면은 미세한 거울(microfacet)들로 이루어져 있다고 본다.
각 microfacet은 서로 다른 방향을 향하고 있으며,
이들이 반사에 기여하는 양은 그 방향(normal)에 따라 다르다.
그런데 이 수많은 방향을 일일이 저장하는 건 불가능하므로,
우리는 이를 확률 밀도 함수처럼 취급해서 모델링한다.
→ 이게 바로 Microfacet Distribution Function, 보통 D(ωₘ) 로 표현된다.
D(ωₘ) 의 의미
- ωₘ: microfacet의 노멀 벡터 (즉, 하나의 거울 조각이 향하는 방향)
- D(ωₘ): 단위 반구 위의 방향 ωₘ 에 대해 그 방향을 향하는 microfacet의 분포 확률
즉, 특정 방향 ωₘ을 향하는 조각이 얼마나 많은지를 말해주는 값.
이상적인 경우
- 만약 표면이 완전히 매끄럽다면?
→ 모든 조각의 노멀은 표면 노멀 n과 같다.
정규화 조건
D(ωₘ)는 확률 밀도이므로, 전체 확률은 1이 되어야 한다.
단, 입사 각도에 따라 조각이 기여하는 면적이 달라지므로,
cos(θₘ)를 가중치로 곱한 적분이 1이 되도록 정규화해야 한다.

이 조건을 만족하는 게 물리적으로 타당한 NDF의 기본 요건이다.
Isotropic vs. Anisotropic Microfacet Distribution
Isotropic (등방성)
- 마이크로패싯의 분포가 방향에 관계없이 동일함.
- 표면을 회전시켜도 산란 거동이 변하지 않음.
- 예: 매끄러운 무광 표면, 균일한 연마 금속 등
Anisotropic (이방성) -> (이번에는 안다룸)
- 마이크로패싯 분포가 방향에 따라 달라짐.
- 예를 들어, 금속판에 연마 방향이 있다면 반사 방향도 그에 따라 길쭉하게 번짐.
- 예: 헤어, 브러시드 메탈, 섬유질 표면
GGX Microfacet Distribution
마이크로패싯 기반 BRDF에서 가장 널리 사용되는 분포 함수 중 하나가 바로 GGX (Trowbridge-Reitz)이다.
이 분포는 매끄러운 금속부터 거친 표면까지 자연스럽게 표현할 수 있는 장점이 있다.

- Wm: 마이크로 노멀
- : 마이크로 노멀의 고도각, 방위각
- αx,αy: X, Y 방향 거칠기 파라미터 (roughness)
- D(ωm): 주어진 마이크로 노멀 방향에 대한 상대적 분포 밀도
핵심 의미
- 거칠기 조절:
- α→0: 완전한 정반사에 가까움 (mirror)
- α→1: 굉장히 거친 표면
- Isotropic 버전은 αx = αy = α일 때 얻어짐
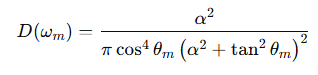
- GGX는 long-tail 특성이 있어서 grazing angle (비스듬한 입사각)에서도 적절히 빛을 반사함
→ 이는 현실적인 재질(금속, 흠집 표면 등)을 표현하는 데 매우 유용
GGX 분포의 특징 – 롱 테일(Long Tail)
Trowbridge-Reitz (GGX) 분포는 입사각이 작을수록(= grazing angle) 반사 기여가 천천히 줄어든다.
이 특성을 롱 테일(long tail)이라고 부른다.
- 다른 분포들 (예: Beckmann)은 θm이 커지면 D(ωₘ)가 급격히 줄어들지만,
- GGX는 θm → 90° 가까워져도 여전히 유의미한 값을 갖는다.
Microfacet 모델에서의 마스킹 함수 (Masking Function)
GGX 분포(또는 그 어떤 마이크로패싯 모델이라도)는 단순히 D(ωₘ)만으로는 물리적으로 일관된 BRDF를 만들 수 없음.
왜냐하면, 특정 방향에서 관측되는 마이크로패싯들은 항상 전부 보이는 게 아님
이 중 일부는:
- 자기 뒷면을 향하고 있거나 (backfacing)
- 다른 마이크로패싯에 의해 가려질 수 있음 (occlusion)
이런 경우, 그 마이크로패싯은 해당 방향에서 반사를 제공하지 못하고.
따라서 이걸 보정해주는 게 바로 마스킹 함수 G₁(ω, ωₘ)이다.
- G₁(ω, ωₘ)는 방향 ω에서 법선 ωₘ을 가진 마이크로패싯이 보이는지 판단
- 값은 항상 0 ≤ G₁ ≤ 1 사이
- G₁ = 1이면 완전히 보임, G₁ = 0이면 가려져 있음
우리가 보는 방향에서 평평한 표면(dA)은 dA * cos(θ) 만큼 보임
microfacet들이 막 울퉁불퉁하게 분포해 있을 때는, 그 microfacet들 중 일부만 실제로 보임.
→ 이 보이는 microfacet의 면적 합이 정확히 cos(θ)가 되도록 보정해야 함
수식으로 표현하면:

- D(ωₘ)은 microfacet들이 어떤 방향으로 분포하는지를 나타내는 함수
- G₁(ω, ωₘ)은 방향 ω에서 ωₘ방향을 가진 마이크로패싯이 실제로 보일 확률 (0~1)
- max(0, ω · ωₘ)은 보정: 뒤돌아 있는 microfacet은 빼자
- 적분 결과는 cosθ, 우리가 보는 면적만큼 되어야 함
렌더링 수식에서 마이크로패싯을 쓰려면, 보이는 면적만큼만 기여하게 해야 함.
- 보이지 않는 면도 계산에 포함돼서 에너지가 과잉산출됨 (빛이 더 많이 보임 → 비현실적)
- 에너지 보존 안 됨 → 비물리적 결과 발생
하지만
마이크로패싯 분포 D(ωₘ)만 가지고는 G₁(ω, ωₘ)을 알 수가 없음
즉, 우리가 어떤 식으로 마스킹되는지를 알려면 표면의 세부 형상(지오메트리)까지 알아야 함
→ 현실적으로는 힘들기 때문에, 모델 기반의 G₁ 함수를 사용해 근사함.
대표적으로:
- Smith G1 함수
- Schlick-GGX 마스킹 모델
Smith 마스킹 근사
복잡한 실제 표면은 너무 많은 microfacet들로 구성되어 있어서,
각 facet이 가려졌는지 아닌지를 정확히 계산하는 건 비현실적임
그래서 통계적으로 독립된 조각들로 모델링함 (→ microfacet theory)
이때 masking은 단순히 ω (관측 방향) 에만 의존한다고 가정함
이게 바로 Smith’s Approximation
수식 전개 과정
원래의 적분 조건에서
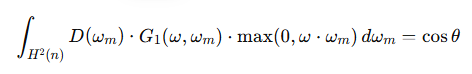
smith 근사를 적용하면
에 의존하지 않고 밖으로 빼냄
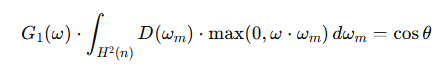
따라서

이 적분식은 마이크로패싯 분포 D(ωm)에 따라 바뀌는데,
Trowbridge-Reitz (GGX) 같은 모델은 이 적분을 해석적으로 풀 수 있음
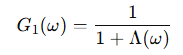
Smith 모델의 핵심 표현이 이거임
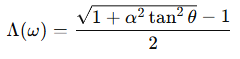
- α: roughness (거칠기), GGX의 핵심 파라미터
- θ\: 관측 방향과 법선 사이의 각도
- tan^2: 표면과 빛/뷰 방향의 기울기 표현
- 이 함수는 θ가 작으면 거의 0, 클수록 값이 커짐 (→ grazing angle에서 마스킹 강해짐)
이 공식이 의미하는 것
- 는 관측 방향에서 얼마나 많은 마이크로패싯이 가려지는지를 수학적으로 표현함
- 결과적으로 입사각이 커질수록 마스킹되어 기여도가 줄어듦
핵심 개념: 마스킹과 섀도잉
- 마스킹(Masking): 관찰 방향 ωo 기준에서 가려지는 마이크로패싯
- 섀도잉(Shadowing): 광원 방향 ωi 기준에서 가려지는 마이크로패싯
이 둘은 각각 다른 방향에서의 가려짐을 나타냄.
수식 정리
- 앞에서 구한 단일 방향 마스킹 함수:

- 최종적으로 마스킹-섀도잉을 모두 고려하면

둘 다 independent라고 가정하고 확률처럼 곱해버림. 이건 Smith 모델의 근사법
샘플링의 핵심: 보이는 마이크로패싯 분포
렌더링에서 마이크로패싯 기반 BRDF를 샘플링할 때, 단순히 D(ωₘ) 분포만 샘플링하면 충분하지 않다
실제 렌더링 적분에 들어가는 분포는 보이는(Visible) 마이크로패싯 분포다.
마이크로패싯 이론이 원하는 샘플링 대상
입사 방향 ω에서 보이는 마이크로패싯의 분포는 다음과 같은 확률 밀도 함수(PDF)를 따라야 한다:

- D(ωₘ): GGX 등으로 표현되는 전체 마이크로패싯 분포
- G₁(ω): 현재 방향에서 보이는 마이크로패싯의 비율 (마스킹)
- ω · ωₘ: 입사 방향과 마이크로패싯 노멀 간의 내적 (입사각)
이 세 가지를 모두 고려한 분포를 샘플링해야, 실제 렌더링 적분에 정확하게 대응할 수 있다.
결국, 이걸 그대로 곱한 분포로부터 마이크로패싯 노멀 ωₘ을 샘플링하는 것이 목표다.
결국
- 표면에 실제로 레이를 쏴서 마이크로패싯과 교차할 필요 없음
- 확률적으로 마치 교차한 것처럼 샘플을 뽑아낼 수 있음
- 이걸 구현한 게 흔히 말하는 GGX VNDF 샘플링이다
마이크로패싯 분포 D(ωm) 자체는 전체 마이크로 패싯의 방향 분포를 표현할 뿐이다.
하지만 실제로 우리가 샘플링해야 하는 건 보이는 마이크로패싯,
즉 특정 입사 방향 ω에서 실제로 광선과 교차 가능한 마이크로패싯만을 고려한 분포다.
이걸 수식으로 표현하면 다음과 같다:

- 특정 방향 ω에서 보이는 마이크로패싯의 확률 밀도 함수(PDF)
- 실제 입사각과 거칠기, 마스킹 정도까지 모두 반영된 샘플링 분포
- 총합이 1이 되도록 정규화된 확률 분포 (pdf)
이 정의는 보이는 마이크로패싯의 방향 분포를 정확히 설명해주지만,
이걸 실제로 샘플링하는 건 또 다른 문제다.
보통 이런 분포에서 샘플을 뽑으려면 inversion sampling을 사용하지만,
GGX visible normal 분포는 수학적으로 너무 복잡해서 정적분의 역함수가 존재하지 않는다.
이 문제를 해결하기 위해 기하학적인 접근법을 택한다.
GGX 분포는 잘린 구(sphere) 혹은 타원체(ellipsoid)가 반복된 구조로 정의되기 때문에,
이를 기반으로 간단한 투영 기하학(hemisphere → disk)을 활용하여 샘플을 생성한다.

아오 드디어 드디어
Torrance–Sparrow 모델: 러프 서피스를 위한 BRDF
드디어 지금까지의 모든 과정을 바탕으로, 러프 서피스의 정반사를 어떻게 처리할 수 있는지를 설명할 수 있다.
PBRT에서는 이를 Torrance–Sparrow 모델이라 부르고,
실제 구현은 마이크로패싯 이론과 Visible Normal Distribution 기반으로 수행된다.
이 모델은 다음의 직관적인 3단계로 구성된다:
- 보이는 노멀 샘플링
관측 방향 ωo 기준으로 보이는 노멀 ωm을 샘플링한다.
즉, Dωo 분포를 따른다.
→ 카메라가 보게 되는 마이크로패싯의 평균적인 방향을 정한다. - 정반사 계산 + 프레넬 적용
ωm을 기준으로 정반사 방향을 구하고 → 입사 방향 ωi를 유도한다.
이때 프레넬 계수 F(ωi,ωo)를 곱해서 빛의 강도를 결정한다. - 마스킹/섀도잉 적용
마이크로패싯 간 가려짐을 고려해 G1(ωi)를 곱한다.
이는 샘플된 마이크로패싯이 다른 패싯에 의해 그림자지는지를 확률적으로 반영한 것.
다시 정리 해보면
- 거친 금속은 실제로는 수많은 미세 거울이 뒤엉켜 있는 상태
- 우리는 그 중에서 관측 가능한 미세 패싯을 확률적으로 샘플링함
- 그리고 그 미세 패싯에서 반사되는 광경을 계산해 에너지 보존을 만족하는 BRDF를 얻는다
샘플된 ωm에서 입사 방향 ωi 구하기
이전까지는 보이는 마이크로패싯 법선 ωm을 샘플링하는 과정이었다.
하지만 렌더링 식에 들어가는 건 실제 빛이 들어오는 방향 ωi
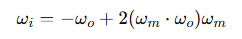
카메라 방향(ωo)과 마이크로패싯 법선(ωm)을 이용해,
그 미세 거울에 반사되어 들어온 방향(ωi)을 계산하는 식이다.
, ωo가 이미 주어졌으면 이걸로 ωm
이건 단순히 두 벡터 사이의 half-vector(절반 방향 벡터)를 구하는 것
→ Cook-Torrance 모델에서 이 half-vector는 매우 중요한 역할을 하게 된다.
Half-vector와 입사 방향 간의 확률 밀도 변환
지금까지는 보이는 법선 ωm을 샘플링한 뒤,
정반사 법칙을 통해 입사 방향 ωi를 계산했었다.
하지만 실제로 BRDF를 계산할 때 필요한 것은
ωi에 대한 확률 밀도 함수 p(ωi) 다.
즉, 우리는 다음을 알아야 한다:
ωm을 어떤 확률로 샘플링했을 때, ωi는 어떤 확률로 나타나는가?
이건 변수 치환에 따른 PDF 보정 문제다.
수학적으로는 Jacobian이 등장한다

이 Jacobian 항은 확률 공간에서의 기하학적 왜곡 보정이라고 생각하면 된다.
즉, ωm을 균등하게 뽑았더라도, ωi 공간에서는 왜곡된 분포로 나타날 수 있기 때문.
을 샘플링해서 ωi를 유도했다면,
BRDF에서의 PDF는 반드시 Jacobian을 곱해서 변환해줘야 한다.
그렇지 않으면 에너지 보존이 깨지고, 샘플링 정확도도 무너진다.
Monte Carlo 적분에서 중요한 건 항상 샘플링된 값의 확률 밀도(PDF) 이다.
문제는 우리가 실제로 샘플링한 건 ωm,
하지만 BRDF 적분 수식은 ωi에 대한 PDF를 요구한다는 점.
이런 경우 변수 치환 공식이 등장한다:

즉, PDF도 기하학적으로 어떻게 왜곡되는지를 고려해서 바꿔줘야 함.
이 보정 항이 바로 Jacobian determinant.
렌더링 이론에서는 이 보정 항이 다음처럼 유도된다

이 수식은 BRDF의 GGX 구현에서 매우 자주 등장하며,
microfacet 모델에서의 reflection geometry를 고려한 정확한 보정 항이다.
요약
- 우리가 샘플링한 건 ωm
- 필요한 건 ωi에서의 PDF
- Jacobian 보정이 필수
- 결과:

앞서 본 내용들을 종합해서, ωi방향에서의 확률 밀도는 다음과 같이 계산된다:
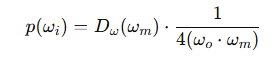
- : visible normal distribution, 즉 가려지지 않은 마이크로패싯 노멀의 밀도
- Jacobian 보정 항, half-vector 기반에서 입사 방향으로의 변환
드디어 brdf완성
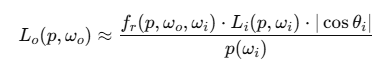
- fr: BRDF
- Li: 입사 복사도
- cosθi: 기하적 감쇄
- p(ωi): 샘플링 PDF
우리가 앞에서 했던 visible normal 기반의 샘플링 루틴이 물리적으로 타당하려면,
BRDF가 이 몬테카를로 근사와 정확히 일치해야함
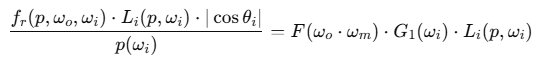
정리하면
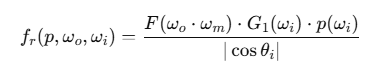
최종적으로 GGX 기반 Torrance–Sparrow BRDF는 이렇게 정의될 수 있음
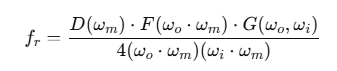
이 구조가 나오려면 샘플링 확률 p(ωi), 마스킹 함수 G, 프레넬 함수 F가 모두 잘 연결되어야 함.

유도 과정 요약
- 가시 노멀 샘플링: 관측 방향 ωo기준에서 Dω(ωm)로부터 노멀 ωm을 샘플링
- 반사 방향 계산
- PDF 보정
- 렌더링 방정식과 정합성 유지: 위 PDF를 사용한 Monte Carlo 근사와 일치하도록 fr를 정의해야 함
- G 항 보정: 단일방향 G1을 곱하는 대신, 쌍방향 G(ωi,ωo)로 대체 (Heitz)
우리가 지금까지 살펴본 Torrance–Sparrow 모델은 마이크로패싯 기반의 반사 이론을 바탕으로,
러프 서피스 위의 정반사를 정확히 모델링할 수 있도록 해준다.
하지만 실제 렌더링 시스템에 이 모델을 그대로 적용하기엔 몇 가지 실용적인 문제들이 존재한다:
- Fresnel 방정식은 계산이 복잡하다.
- Microfacet 분포와 마스킹/섀도잉 함수는 다양한 형태가 존재한다.
- 샘플링과 PDF 보정까지 고려하면 구현 난이도가 높다.
이를 실용적인 형태로 정제해 렌더링 시스템에서 직접 사용할 수 있도록 구성한 모델이 바로 Cook–Torrance BRDF다.
Cook–Torrance BRDF는 다음의 세 가지 핵심 요소를 기반으로 구성된다:
- D(ωₘ): Microfacet 분포 함수
→ 보통 GGX (Trowbridge-Reitz) 분포를 사용하여 현실적인 거칠기를 표현 - G(ωᵢ, ωₒ): Geometry term (Masking-Shadowing 함수)
→ Smith 모델 기반의 G₁을 사용하거나, Heitz의 G로 교체 - F(ωᵢ): Fresnel 반사율
→ 실시간 렌더링에선 Schlick 근사식으로 효율적으로 계산
이 세 가지를 조합해 다음과 같은 형태로 BRDF를 정의한다:
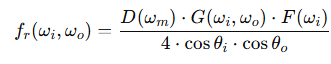
드디어 내가 그냥 가져다만 썼던 수식들이 조금이나마 이해가 간다..
내가 지금 쓰고 있는 조명 모델은 Cook–Torrance BRDF 기반이며,
GGX 분포 함수, Smith 마스킹 함수, Schlick Fresnel 근사를 조합한
PBR(Pysically Based Rendering) 구현이다.
'Computer Graphics > VulkanPT' 카테고리의 다른 글
| pt - 1. (.pbrt)파일 파싱과 나이브한 구현 (0) | 2025.04.28 |
|---|---|
| pt - 0. path tracing 렌더러 시작 (2) | 2025.04.25 |
| The Rendering Equation 정리 (0) | 2025.04.21 |
| Vulkan에 Ray Tracing 도입 하기 (2) (1) | 2025.04.11 |
| Vulkan에 Ray Tracing 도입 하기 (1) (0) | 2025.04.11 |