핵심 요약
1. 렌더링 방정식(Rendering Equation)

이 식은 어떤 표면에서 특정 방향으로 나가는 빛의 세기를 정의하며,
간단히 말하면 "자체 발광 + 다른 지점에서 반사되어 들어온 빛의 총합"으로 구성되어 있다.
여기서 중요한 건 이 방정식이 직접광뿐 아니라 간접광까지 모두 포함한다는 점이다.
2. Neumann 시리즈 전개 방식

렌더링 방정식은 자기 자신을 포함하는 적분 방정식인데, 이를 직접 풀 수 없기 때문에 무한급수로 전개해서 근사한다.
이 방식은 "직접광", "1차 반사", "2차 반사", ... 이런 식으로 빛의 경로를 단계별로 누적해 나가는 구조다.
이런 수학적 구조를 기반으로, 우리가 흔히 말하는 멀티 바운스 라이트를 표현할 수 있다.
3. Monte Carlo 기반의 근사 방법
여기서부터 Path Tracing과 연결된다.
Neumann 시리즈에서 무한히 더해지는 항들을 하나하나 계산할 수는 없기 때문에,
확률적으로 경로를 하나 선택해서(빛이 이동하는 경로를 따라가서) 그 경로가 얼마나 기여하는지를 평균낸다.
이때 경로는 Markov Chain처럼 이전 상태에 따라 확률적으로 다음 상태가 정해지는 구조로 만들어진다.
즉, 여러 샘플을 추출하고 각 샘플마다 "기여도 × 확률 보정"을 해서 평균을 내면, 결국 최종 이미지가 나온다.
이게 바로 우리가 오늘날 쓰는 Path Tracing의 핵심 원리다.
렌더링이란 결국, 빛이 어떠게 표면을 따라 이동하고, 반사되고, 관측되는가를 계산하는 작업이다.
1986년 James Kajiya는 이 과정을 하나의 수식으로 통합 정리했다. 이게 바로 Rendering Equation이다.

I: 점 x'에서 x방향으로 향하는 빛의 세기
g: 시야각, 거리, 가시성등을 포함한 기하학 계수
e: 자체 발광 (emission)
p: x'' -> x' 로 들어온 빛이 x로 반사될 확률
즉 표면에서 특정 방향으로 나가는 빛의 세기는
해당 지점의 자체 발광 + 모든 다른 지점으로부터 반사되어 들어오는 빛의 누적으로 표현된다.
하지만 렌더링 방정식은 자기 참조형 적분 방적식이므로 직접 해석이 불가능하다.
I(x, x') = ... Integral(I(x', x''))...
따라서 수치적으로 근사가 필요한데,
가장 먼저 제안된 방법 중 하나가 Neumann Series이다.
이 방식은 렌더링 방정식을 선형 연산자 형태로 바꾸고, 다음처럼 무한 급수로 전개한다:
Neumann Series


여기서 ge는 직접광 (emissive)
gMge는 한번 반사된 간접광
gMgMge는 두번 반사된 간접광이다.
Neumann 급수는 "한 번 더 반사된 빛을 점점 더 적게 기여하게" 전개되므로, 수렴 조건이 필요하다.
이 수렴 조건은 수학적으로 M 연산자의 스펙트럼 반지름이 1보다 작을 것이다.
렌더링 문제에서는 이 조건이 자연스럽게 만족되며, 결과적으로 다음과 같은 의미 있는 물리 해석이 가능해진다:
빛은 직접 오거나, 한 번 반사되거나, 두 번 반사되거나, 계속 그렇게 누적되어 관측된다.
utah Approximation
Neumann 시리즈는 이론적으로 무한히 반사되는 빛까지 모두 누적하지만,
계산량이 너무 크고, 모든 반사를 고려할 필요가 없는 경우도 있다.
그래서 나온 것이 바로 Utah Approximation이다.
이 방식은 Neumann 시리즈의 앞 두 항만을 취해 다음처럼 근사한다

ge는 직접광
gMe0은 광원에서 나온 빛이 다른 표면에 한 번 반사돼서 오는 빛
이 방식은 고전적인 숨은 표면 제거(hidden surface removal) 문제를 계산하던 초창기 렌더링 기술의 연장선이며,
가볍고 빠른 조명 모델링이 필요한 환경에서는 여전히 유용하다
whitted approximation
Utah 근사에서는 직접광과 1차 반사까지만 고려했지만,
Whitted는 그보다 더 정교한 거울 반사(reflection)와 굴절(refraction)까지 표현하고자 했다.
그래서 그는 다음과 같은 형태의 근사 수식을 제안했다

이 방식은 거울 반사, 굴절, 섀도우 레이까지 표현할 수 있다.
오늘날 우리가 Ray Tracing이라 부르는 기법의 가장 초창기 모델이다.
하지만 확률적 샘플링 없이 결정론적”방식으로 광선을 쏘기 때문에
간접조명(Global Illumination), 소프트 섀도우, 노이즈 기반 부드러운 반사 등을 표현할 수 없다.
Distributed Ray Tracing Approximation
Whitted 모델을 기반으로 샘플링을 확장한 방식이 등장했다.
Cook은 Whitted의 세 가지 레이 분기(디퓨즈, 반사, 굴절)를 유지하면서도,
각 방향을 하나의 값으로 결정하는 것이 아니라 분포(distribution)를 따라 확률적으로 샘플링했다.
부드러운 반사(Glossy Reflection), 소프트 섀도우(Soft Shadow), 모션 블러, 피사계 심도, 텍스처 블러 같은 효과들이 자연스럽게 표현 가능해진다.
Radiosity Approximation
Radiosity 기법은
확산 표면만을 가정한 특수한 형태의 렌더링 접근이다.

B(x')은 점 x'에서 나가는 radiosity 단위 면적당 복사 에너지
모든 표면이 확산 반사만 한다는 가정 하에, 표면 간 에너지 교환을 직접 계산하여 전역 조명을 표현한다.
이는 반사·굴절 등은 처리할 수 없지만, 간접조명과 음영효과를 물리적으로 표현할 수 있는 첫 번째 시도였고,
특히 건축 시각화나 정지 이미지 렌더링에서 오랫동안 널리 사용되었다.
Markov Chain을 이용한 경로 추적 (중요)
Radiosity는 전역 조명의 직접적인 계산을 가능하게 했지만, 확산 표면이라는 강한 제약이 있었다.
이후 등장한 Monte Carlo 기반 경로 추적 방식은 이 제약을 극복하기 위해 확률적 경로의 평균을 통해
렌더링 이퀘이션을 근사하는 새로운 접근을 제시했다.
이 방법은 결국, 빛의 경로를 확률적으로 따라가며, 각 경로가 기여하는 조명을 누적하여 전체 이미지를 만들어낸다.
벡터 방정식으로 다음과 같이 표현한다

x: 조도값
a: 직접 조명
M: 조명 전이 행렬 (reflectance, geometry)
뉴만 시리즈로 전개하면
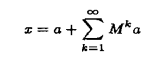
이 무한급수를 Markov Chain 기반 경로로 근사하는 것이 논문이 제안하는 핵심 Monte Carlo 방식이다.
Kajiya는 이 전이 연산자 M을 확률적인 경로로 변환하고,
샘플 경로마다 누적되는 빛의 기여를 평균내어 최종 색을 계산할 수 있다고 보았다.
이는 이후 등장하는 Path Tracing, Bidirectional Path Tracing, Metropolis Light Transport 등의 기초 이론이 된다.
수렴 조건을 만족한다면, 위 무한합을 경로 평균으로 바꾼다.
이때, 각 경로는 다음과 같은 확률로 선택된다.

n0: 광원에서 출발
nk: 카메라 혹은 관측점에 도달
각 경로는 Markov Chain처럼 확률적으로 생성됨
이때 중요한 점은,
경로 ω 는 고정된 것이 아니라 확률 분포 p(ω) 를 따라 샘플링된다는 점이다.
이 기대값 수식은 Monte Carlo Integration의 일반적인 형태와 정확히 일치한다:

경로 ω를 따라 빛이 이동하면서 축적되는 에너지를 다 곱해서
마지막에 광원 세기를 곱하고
그걸 샘플링 확률로 나눈다
앞서 설명한 Markov Chain 기반의 기대값 수식을 실제로 적용하려면, 각 경로 ω에 대해 다음 과정을 반복해야 한다.
이 절차는 논문에서 명시한 무한 차원(Monte Carlo) 근사 방법을 기반으로 한다.
1. 관측 지점에서 시작
- 렌즈 또는 이미지 평면 상의 픽셀 위치 x 하나 선택한다.
- 이 픽셀로부터 렌즈 통과 방향 또는 뷰 레이 하나를 샘플링한다.
2. 장면 내에서 광선과 교차하는 점 x′를 찾는다
- 이 교차점이 바로 x′이며, 실제 표면 위의 점이다.
- 이때부터 방사선을 따라가며 경로를 확장한다.
3. 방사선 기여도 누적

각 단계마다 다음 항을 계산한다:
- 기하학 계수 : 시야각, 거리, 가시성 포함
- BRDF 또는 반사율 ρ
- 발광 계수 ε– 광원이면 포함됨
- 각 기여를 곱하고 누적 → 픽셀에 반영
이 과정은 결국 Markov 경로 하나당 한 번의 색상 샘플을 만드는 구조
많은 경로를 반복해서 평균을 내면, 렌더링 이퀘이션의 근사값에 점점 가까워짐
기존 radiosity 방식과 다르게, 가시성이 없는 표면은 아예 기여하지 않기 때문에 더 효율적임
이후 내용
실제 결과와 함께 렌더링 구현을 위한 세부 샘플링 전략과 성능 비교를 설명한다
- 랜덤 변수 기반 경로 샘플링
각 픽셀, 표면, 조명에서 랜덤 방향을 선택해 경로를 구성함.
→ 지금의 Path Tracing과 거의 동일한 구조. - importance sampling 적용 가능성 언급
하지만 당시 구현에서는 적용하지 않았고, 샘플 수는 고정(40 paths per pixel)으로 사용됨. - Whitted-style vs Integral-style 결과 비교
그림자, 반사, 반투명 영역에서 통합식 기반 경로 추적이 더 부드럽고 사실적인 결과를 보여줌. - 컴퓨팅 자원 소모 비교
IBM 기기에서 수백 분의 시간이 소요되며, 당시 기준으로는 매우 고비용.
여기까지는 렌더링 이퀘이션을 수식으로 어떻게 풀 수 있냐,
그걸 경로 기반으로 어떻게 근사하냐는 얘기였고,
이제 진짜 중요한 건 그 경로를 어떻게 잘 뽑느냐인데
논문에서도 뒤에서 그 중요성을 강조하면서
샘플링 전략이나 분포에 따른 효과들을 설명하고 있지만,
내가 구현하는 방식은 BRDF에 기반한
Importance Sampling 쪽이라 생략하고 다음 포스트에서 함께 써야겠다.
'Computer Graphics > VulkanPT' 카테고리의 다른 글
| pt - 0. path tracing 렌더러 시작 (0) | 2025.04.25 |
|---|---|
| BRDF 정리 (0) | 2025.04.22 |
| Vulkan에 Ray Tracing 도입 하기 (2) (1) | 2025.04.11 |
| Vulkan에 Ray Tracing 도입 하기 (1) (0) | 2025.04.11 |
| Vulkan에 Ray Tracing 도입 하기 (0) (0) | 2025.04.11 |