레퍼런스

복습
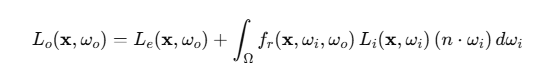
모든 렌더링은 이 렌더링 방정식을 푸는 것으로 시작
렌더링 방정식은 순환 적분식 구조이므로 직접푸는 것은 불가능
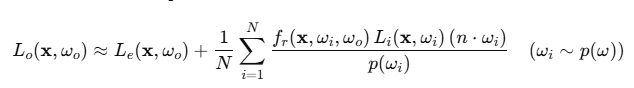
따라서 몬테카를로와 같은 근사식으로 렌더링 방정식을 근사

path tracing은 경로 하나만 샘플링하여 그 경로하나가 전체 적분 값을 대표하도록 처리
기존 구현 방식
초기에는 BRDF 중요도 기반 샘플링을 통해 path tracing을 구성
BRDF로 샘플링한 방향이 우연히 광원에 도달하면
그때만 throughput × radiance를 계산하는 방식
- BRDF 샘플링 → 경로 따라 ray를 쏨
- 광원에 닿을 때까지 bounce
- 맞으면 그때만 기여 누적
문제점
- 1 SPP에서 광원에 도달하지 못하면 그 샘플이 버려짐
- 노이즈가 심하고 수렴이 느림
NEE (Next Event Estimation) 추가

NEE는 ray가 광원에 맞을 때를 기다리지 않고
맞은 지점에서 직접광을 샘플링하여 즉시 조명 기여를 평가하는 방식
기대 효과
- 1 SPP에서도 광원이 보이는 위치라면 직접광 기여를 누적 가능
- 따라서 노이즈가 줄고 수렴이 훨씬 빨라짐
NEE는 다음과 같은 순서로 수행
- 현재 위치에서 scene 내 광원 중 하나를 무작위로 선택 (광원에 모양이 있어 삼각형으로 전부 쪼개서 저장) 즉 광원 삼각형을 선택
- 선택한 광원의 면적 중 한 점을 sampling
- 해당 위치를 향해 shadow ray를 하나 발사
- 그 경로가 가려지지 않았다면 → BRDF를 통해 기여량 계산
- 계산된 조명 기여를 현재 throughput에 곱해 누적
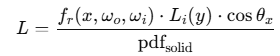
pdf 계산
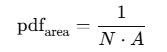
광원중 하나 x 면적

후에 나올 brdf의 계산은 입체각 기준이기 때문에 입체각 기준으로 계산
따라서

- cos x 레이를 쏘려는 지점에서 법선 방향과 레이의 내적
- cos y 광원 지점에서의 법선 방향과 레이의 내적
- pdf: light sampling 시 해당 방향으로 샘플될 확률
주의점

같은 조명 기여가 두 경로에서 중복 계산 될 수 있음
결과가 편향될 수 있음 -> 노이즈 증가
따라서 MIS(Multiple Importance Sampling) 사용
MIS란? 여러 샘플링 전략이 동일한 기여를 만들 수 있을 때
중복 없이, 편향 없이 합산하기위한 방법
Balance Heuristic

샘플링한 레이를 brdf 기준으로 계산한 pdf와 balance heuristic
따라서 최종 NEE기여는

NEE추가해서 나온 이미지




svgf 도입 중
이제 path tracing 결과를 기반으로 실시간 렌더링을 노려보고자 SVGF를 도입
논문을 열심히 읽고 구현하긴 했는데 자의적으로 해석한 부분이 있을 수도 있음,,,
구현 목표
1. 낮은 샘플 수에서 빠르게 수렴
2. 카메라 이동이나 씬 변화에도 노이즈가 안정적으로 억제
우선 전체적인 개요

path tracing 결과는 직접광과 간접광으로 나눠서 처리
- 직접광은 NEE를 통해 직접 샘플되기 때문에 신뢰도가 높고, variance가 낮음
- 간접광은 bounce를 여러 번 거쳐 얻어진 결과이므로 variance가 높고, 노이즈도 많음
따라서 두 성분을 같은 필터 강도로 처리하면 비효율적이기 때문에 나눠서 처리
필터링을 하기 전, 먼저 radiance를 albedo로 나눈다.
- radiance에는 texture 색 정보가 곱해져 있는데 이 상태로 필터링하면 텍스처 디테일까지 뭉개짐
- 따라서 필터링 전에는 albedo를 제거해서 색 정보를 분리 -> 필터링 후에는 다시 albedo를 곱해서 원래 색을 복원
이 과정을 통해 노이즈는 줄이되 텍스처 디테일은 유지할 수 있음
그 다음에 직접광 간접광 각각 필터링
그 다음 필터링한 두 이미지를 합치고 다시 albedo를 곱해서 원래 색을 복원
그 뒤 톤 매핑과 안티엘리어싱

1. Temporal Accumulation
우선 1 spp path tracing 결과를 프레임 간 누적
- 이때 단순히 과거 프레임 색을 복사하지 않고,
- Motion Vector, Normal, Depth, Mesh ID를 이용해 이전 프레임 값이 현재 픽셀과 같은 지점에서 온 값인지 판단
일치도 판단 방식
- 재투영된 위치를 기준으로 2×2 주변 픽셀을 bilinear 보간
- 각 픽셀의 Normal, Depth, Mesh ID를 비교
- 4개 중 하나라도 일치하면 → 가중 평균으로 누적
- 4개 모두 일치 안 하면 → 3×3으로 범위 확장
- 그래도 없으면 → 재시작 (이전 값 무시)
누적 방식: EMA (Exponential Moving Average)
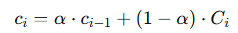
α: blending weight
ci-1: history color 이미지 (필터의 1step 결과물)
이 방식은 오래된 샘플은 점점 희석되지만 빠르게 수렴하기 때문에 실시간 렌더링에 적합
-> 이제 많이 누적된다고 화면 개선이 되진 않는다.
2. 분산 추정
이 단계에서는 누적된 샘플들의 시간 변화량을 분석하여, 해당 픽셀에 노이즈가 얼마나 있는지를 판단
- 분산이 크다 → 샘플들이 시간에 따라 많이 흔들렸다 → 노이즈가 많을 가능성 높음
- 분산이 작다 → 결과가 시간에 따라 안정적이다 → 노이즈가 적음
분산을 추정하기 위해, 다음 두 값을 시간 축 누적 방식으로 저장
- 휘도의 평균 (mean of luminance)
- 휘도의 제곱 평균 (mean of luminance²)
이 두 값을 가지고 고전적인 분산 계산 방식

을 통해 분산을 구함
구현 방식
이전 프레임에서 누적해둔 휘도의 평균 , 휘도의 제곱 평균을 현재 프레임에서 motion vector로 재투영하여 불러온 뒤
재투영 유효성 판별(=일치도 검사)은 Temporal Accumulation과 동일하게 수행하고
이 결과를 바탕으로 현재 픽셀의 분산을 계산
여기서 계산된 분산은 뒤에 필터에서 weight 계산하기위해 들어 간다.
샘플수가 적을 때 (spp < 4)
누적된 샘플 수가 너무 적다면 분산 값은 신뢰할 수 없다.
이 경우엔 분산 기반 필터를 사용하지 않고
7x7 bilateral 필터를 fallback으로 적용 (depth, normal만 사용)
3. a-torus wavelet 필터
노이즈를 제거하면서도 경계를 보존하는 필터링 기법
특징은 픽셀 사이를 건너뛰며 필터링 커널을 적용하는 방식을 사용

- 1스텝: 이웃한 픽셀 (stride = 1)
- 2스텝: 1칸 건너뛰며 필터 적용 (stride = 2)
- 3스텝: 2칸 건너뛰며 적용 (stride = 4)
스텝이 진행될수록 더 넓은 범위를 필터링 가능
A-Trous 필터는 픽셀 주변 이웃들과의 유사도를 판단해
가중 평균(weighted average)을 통해 radiance 값을 보간
- Normal weight: 물체 표면의 방향이 비슷할수록 높은 가중치
- Depth weight: 깊이 차이가 작을수록 높은 가중치
- Variance weight: 노이즈가 적을수록 더 신뢰할 수 있는 샘플

- h(q)는 커널 내 위치 q에 대한 spatial weight, h = {1/16, 1/4, 3/8, 1/4, 1/16}
- w(p,q)는 normal / depth / variance 기반 유사도 가중치,

- ci(q)는 이전 스텝의 radiance 값
이 수식은 주변 픽셀들과의 유사도(weight)를 기반으로 한 가중 평균 필터
A-Trous 필터는 radiance 값뿐 아니라, 해당 radiance의 신뢰도인 분산(variance)도 함께 필터링

필터링이 반복될수록 각 픽셀의 값은 주변과 섞여서 바뀌기 때문에,
그에 맞게 분산도 새로 계산되어야 정확한 weight 추정이 가능하기 때문
총 5스텝까지 적용
각 스텝마다 stride를 키우면서 더 넓은 영역까지 노이즈를 억제
- 1스텝: 가까운 노이즈 제거 (디테일 유지) -> history color 이미지로 저장
- 5스텝: 넓은 영역의 저주파 노이즈까지 제거 -> 출력 이미지
4. Edge-stopping functions
여기서 시그마는 보정 계수인데
σz = 1, σn = 128, σl = 4,
1. depth

- σz = 1
- 깊이 차이가 클수록 weight를 낮게 설정
- 분모에 있는 ∇z⋅(p−q)는 로컬 depth gradient에 따른 보정
- depth 차이만 보면 무조건 경계인데
- 원래 그방향이 깊이 변화가 좀 있는 방향이면 그만큼 더 허용해줌
2. normal

σn = 128
법선 방향이 다르면 같은 표면이 아닐 가능성이 높으므로 weight를 급격히 줄여 강하게 억제.
3. luminance

- 분산 자체가 노이즈가 커서 가우시안 블러로 먼저 부드럽게 적용 후 사용
- a torus 들어가기 직전에만 사용 -> 갱신될 때마다 사용하지 않음
- 분산이 크면 → 이 픽셀 자체가 noisy → 밝기 차이에 덜 민감하게 필터링
- 분산이 작으면 → 이 픽셀은 안정됨 → 밝기 차이에 더 민감하게 대응

아까 정리했듯 분산은 필터내에서 스텝마다 갱신된다.
현재 구현된 내 파이프라인
1. Path Tracing
- G-buffer 생성 - primary ray로 gbuffer생성
- Normal
- Depth
- Albedo
- Mesh ID
- 이전 카메라 정보를 받아 이전 프레임의 normal depth meshID과 일치도 판별을 하여 누적or갱신 판단
- 현재 픽셀 월드 위치 -> 이전 카메라로 스크린 변환을 거쳐 -> 이전 픽셀 좌표 예측
- 픽셀 기준으로 먼저 2x2개의 픽셀 가져옴 -> 조건 만족하는 픽셀만 누적 평균
- 없으면 3x3 -> 이래도 없으면 초기화
- 누적/분산 계산을 위한 이미지 생성
- Sample Count: 픽셀당 분산이 얼마나 누적되었는지 저장
- Moment1: 직접광 / 간접광 각각 휘도의 평균
- Moment2: 직접광 / 간접광 각각 휘도의 제곱 평균
- 출력 결과
- Direct history + 1spp direct 샘플 ema누적 결과, a = 0.05
- Indirect history + 1spp indirect 샘플 ema누적 결과, a = 0.05
- Direct/Indirect 각각의 분산 맵 + 샘플에 누적된 픽셀 수 -> (spp < 4) 판단
2. 3×3 Gaussian 필터
- 직접광, 간접광 각각의 분산 이미지에 한 번만 적용
3. A-Trous Wavelet 필터
- Direct / Indirect 각각 독립적으로 필터링 수행
- 총 5 스텝 반복, stride는 1 → 2 → 4 → 8 → 16
- 1스텝 결과는 history buffer로 저장 (다음 프레임 누적용)
- 5스텝 결과가 최종 필터링된 radiance 출력
- spp < 4 일 경우 normal, depth 로만 7x7필터
1step 만 진행로 5step 진행
4. Composite
- 필터링된 Direct + Indirect 결과를 합산하고,
- 최종적으로 Albedo를 곱해서 최종 색을 복원
현재는 Tonemapping과 TAA(Temporal Anti-Aliasing)는 아직 미구현 상태
결과


전반적으로 문제인데 가장 도드라지는 문제점 몇가지를 뽑아보면
1. 색 번짐 (Albedo 복원 후 문제)
바닥이나 세면대처럼 색이 있는 오브젝트에서
알베도를 나눴다 다시 곱하면 푸른빛이 번진다.
특히 normal이 비슷한 엣지 주변에서 색상이 번짐
→ 필터 가중치 계산식 확인 필요
2. 수렴 불안정 / 잔상 울렁거림
한 샘플의 영향이 크다 보니 전체 화면이 울렁거린다.
EMA 계수를 0.05까지 낮춰도 완전한 안정성은 부족하다.
→ 샘플링 전략과 누적 방식 재검토 필요
3. 거울 반사 영역 블러 현상
거울이나 반사 재질의 결과가 흐려지고 퍼져 보인다.
날카로운 반사 디테일이 유지되지 않음
→ 재질별 필터 강도 조정 또는 제외 처리 고려
'Computer Graphics > VulkanPT' 카테고리의 다른 글
| pt - 10. NEE 계산 수정, svgf 디모듈레이션 수정, 필터에서 거울만 수정 (1) | 2025.05.15 |
|---|---|
| pt - 9. 푸른 빛 원인 찾음 (0) | 2025.05.14 |
| pt - 7. svgf 필터 추가 (0) | 2025.05.12 |
| pt - 6. 푸른빛 해결, 안티 엘리어싱, 러시안룰렛 추가 (0) | 2025.05.08 |
| pt - 5. 광원 정규화, bloom 적용, NEE 적용 중 (0) | 2025.05.07 |